(IME - 2021/2022)Um prisma possui um nguo agudoe n
(IME - 2021/2022)
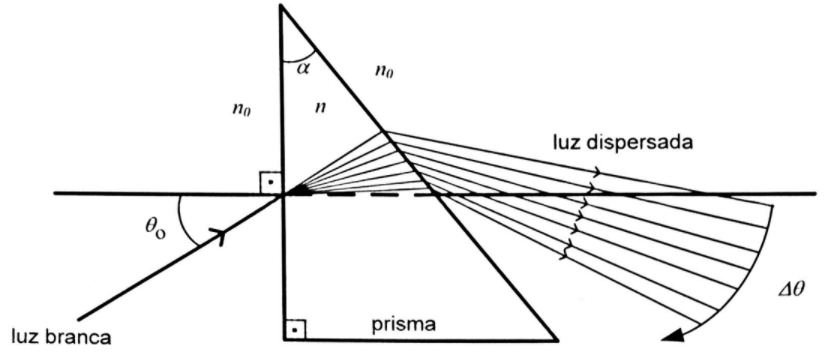
Um prisma possui um ânguo agudo \(\alpha\) e índice de refração variável de acordo com a expressão:
\(n (\lambda) = A + \frac {B}{\lambda ^2}\)
em que A e B são constantes e \(\lambda\) é o comprimento de onda.
Uma luz branca vinda do ar (\(n_0 = 1\)) incide sobre a face vertical do prisma e sofre dispersão cromática no seu interior, voltando para o ar ao sair do prisma. Tal luz, possui componentes espectrais no intervalo: \(\lambda _1 \leq \lambda \leq \lambda _2\).
Consideração:
- Os ângulos \(\theta _0\) e \(\alpha\) são tão pequenos que a aproximação \(sen (x) \cong x\) é válida, para \(x = \theta _0\) ou \(x = \alpha\).
Diante do exposto, a maior abertura angular \(\Delta \theta\) entre as componentes espectrais é aproximadamente:
\(\frac {\alpha A (\lambda ^2 _2 - \lambda ^2 _1)}{\lambda _1 \lambda_2}\)
\(\frac {\theta_0 A (\lambda ^2 _2 - \lambda ^2 _1)}{\lambda _1 \lambda_2}\)
\(\frac {\alpha B (\lambda ^2 _2+ \lambda ^2 _1)}{(\lambda _1 \lambda_2)^2}\)
\(\frac {\theta _0 B (\lambda ^2 _2- \lambda ^2 _1)}{(\lambda _1 \lambda_2)^2}\)
\(\frac {\alpha B (\lambda ^2 _2- \lambda ^2 _1)}{(\lambda _1 \lambda_2)^2}\)


