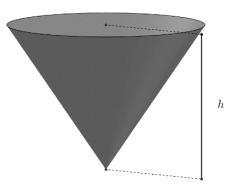
(UFPR - 2023) Na figura ao lado, tem-se um reserva
(UFPR - 2023) Na figura ao lado, tem-se um reservatório no formato de um cone circular reto com altura \(h\) e área do topo igual a \(12\ m^2\). Esse reservatório está sendo preenchido com um líquido cujo volume em \(m^3\) é dado por:
\(V(t)=log_2(t^2+1)\)
sendo \(t\geq 0\) o tempo. Em quanto tempo o líquido atingirá metade da capacidade desse reservatório?
A
\(t= \sqrt{ 4^h-1}\).
B
\(t= 2^h-1\).
C
\(t= \sqrt{ 2^h-1}\).
D
\(t= 4^h-1\).
E
\(t=\sqrt{4^h+1}\)


