(UNICAMP - 2022 - 2 fase)Por volta de 1845, o mate

(UNICAMP - 2022 - 2ª fase)

Por volta de 1845, o matemático belga Pierre Verhulst começou a estudar um tipo de função que hoje é conhecida como função logística. Originalmente utilizada para modelar problemas envolvendo crescimento populacional, atualmente tem muitas outras aplicações em ecologia, biomatemática, sociologia e ciências políticas. Uma função logística pode ser definida por

\(f(x ) = \frac {L}{1+2^{-k(x-x_0)}} , \ \ \ \ \ x \epsilon \mathbb{R},\)       

em que \(k > 0, \ L > 0\)  e  \(x_0 \epsilon \mathbb{R}\)

 

a) Seja \(f^{-1}\) a função inversa de 𝑓. Determine a expressão e o domínio de \(f^{-1}\).

 

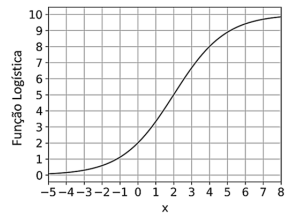
b) O gráfico abaixo é de uma função logística com 𝐿 = 10. Determine os valores de \(x_ 0\)  e 𝑘.