(ITA - 2022 - 2 fase)Sejae denote pora parte imagi

(ITA - 2022 - 2ª fase)

Seja \(z \ \epsilon \ \mathbb{C}\) e denote por 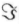\((z)\) a parte imaginária de \(z\). Determine todos os possíveis \(z \ \epsilon \ \mathbb{C}\) com 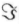\((z) \neq 0\) tais que temos simultaneamente 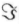\((z^3) = 0\) e 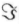\(((1+z)^3) = 0\).