(AFA - 2008)As funes f: do 1o grau e g: [b, +[ do
(AFA - 2008)
As funções f: \(\mathbb{R}\rightarrow \mathbb{R}\) do 1o grau e g: \(\mathbb{R}\rightarrow\) [b, +\(\infty\)[ do 2o grau estão representadas no gráfico abaixo.
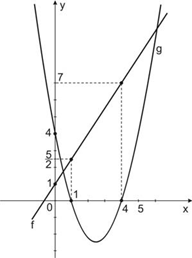
Com base nas informações acima, é correto afirmar que
A
o menor valor de b que torna a função g sobrejetora é um número inteiro.
B
(gogof -1) (\(\frac{5}{2}\)) > 0.
C
\(\frac{[f(x)]^{2}}{g(x)}\) > 0 \(\Leftrightarrow\) {x \(\in \mathbb{R}\) I x < 1 ou x > 4}.
D
f(x) - g(x) \(\leq\) 0 \(\Leftrightarrow\) {x \(\in \mathbb{R}\) I x \(\leq\) 0 ou x \(\geq\) 6}.


