(ITA - 2023 - 1 FASE)Um corpo de massa m lanado em

(ITA - 2023 - 1ª FASE)

Um corpo de massa m é lançado em um plano horizontal sem atrito, sob ação da gravidade g, e, ao entrar em um tubo, executa uma trajetória circular de raio R. A força exercida no corpo pelo tubo logo após o início do movimento circular tem intensidade F. Após meia volta, o corpo percorre uma trajetória retílinea em movimento uniforme até certa distância e depois sobe até certa altura h. O corpo sai do tubo em movimento vertical e imediatamente passa a se mover dentro de um fluido viscoso até atingir altura máxima H, conforme mostra a figura.

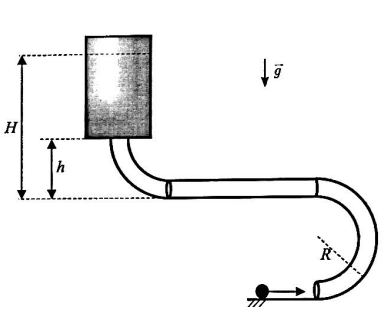
Considere que o corpo se desloca pelo tubo sem atrito; que o diâmetro do tubo é desprezível em relação a R, h e H; e que o módulo do trabalho realizado pela força de atrito viscoso até a massa atingir H é equivalente a um terço da energia cinética da partícula, quando esta adentra o fluido. Assinale a alternativa que expressa H em função das variáveis fornecidas.