(ITA - 2023 - 2 FASE)Considere uma partcula , de m

(ITA - 2023 - 2ª FASE)

Considere uma partícula $P_1$, de massa $m_1$, inicialmente em repouso. Em seguida, essa partícula é acelerada por uma força constante $\underset{F_{1}}{\rightarrow}$, durante um intervalo de tempo $\Delta t_{1}$. Após este intervalo de tempo, $P_1$ move-se livremente sem atrito por um plano, até colidir com uma partícula $P_2$, de massa $m_2 = 2m_1$. Após a colisão, $P_2$ sai em uma trajetória que faz um ângulo de $\theta = \frac{\pi }{6} \ rad$ com relação à trajetória inicial (pré-colisão) de $P_1$. Após um breve deslocamento, uma força constante $\underset{F_{2}}{\rightarrow}$, com direção contrária à da velocidade da partícula $P_2$, atua durante um intervalo de tempo $\Delta t_{2}= \sqrt{3} \Delta t_{1}$ atéa parada total de $P_2$.

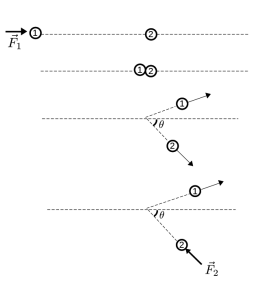
Sabendo que a colisão entre $P_1$ e $P_2$ é inelástica e resulta em uma perda de 25% da energia mecânica do sistema, determine a magnitude da força $F_1$ em termos da magnitude de $F_2$.