(IME - 2022/2023 - 1 fase)Uma fonte sonora est pen
(IME - 2022/2023 - 1ª fase)
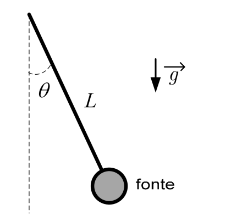
Uma fonte sonora está pendurada por um fio ideal, conforme ilustrado na figura, realizando um movimento pendular.
Dados:
• frequência da fonte sonora: \(f\);
• comprimento do fio do pêndulo: \(L\);
• aceleração da gravidade: \(g\);
• velocidade do som: \(v\).
Se \(\theta_{max}\) é o ângulo máximo atingido pelo fio que sustenta a fonte com relação à vertical, a frequência máxima do som ouvido por um observador localizado a uma distância ínfima do ponto mais baixo da trajetória da fonte é:
\(\frac{fv}{v-{\sqrt{2gL[1-sen(\theta_{max})]}}}\)
\(\frac{fv}{v-{\sqrt{2gL[1-cos(\theta_{max})]}}}\)
\(\frac{f}{v} \{v-\sqrt{2gL[1-sen(\theta_{max})]\}}\)
\(\frac{f}{v} \{v-\sqrt{2gL[1-cos(\theta_{max})]\}}\)
\(\frac{fv}{v-{\sqrt{2gLcos(\theta_{max})}}}\)


